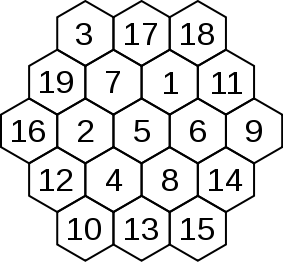
According to Wikki which shows the same hexagon as above:
A magic hexagon of order n is an arrangement of numbers in a centered hexagonal pattern with n cells on each edge, in such a way that the numbers in each row, in all three directions, sum to the same magic constant. A normal magic hexagon contains the consecutive integers from 1 to 3n2 − 3n + 1. It turns out that magic hexagons exist only for n = 1 (which is trivial) and n = 3. Moreover, the solution of order 3 is essentially unique.[1] Meng also gave a less intricate constructive proof.[2]
The order-3 magic hexagon has been published many times as a 'new' discovery. An early reference, and possibly the first discoverer, is Ernst von Haselberg (1887).
Although there are no normal magical hexagons with order greater than 3, certain abnormal ones do exist. In this case, abnormal means starting the sequence of numbers other than with 1.
In other words, as M ("Sit down 007") is known it's fairly easy to work out the sequence of numbers on the rows, a bit like a variation on the magic square - a square with the corners knocked off if you like!